Derivation of PV=nRT (Ideal Gas Law)

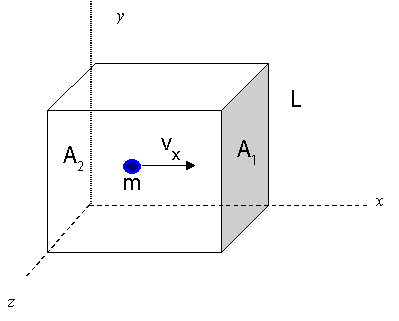
To begin, let's visualize a rectangular box with length L, areas of ends A1 and A2. There is a single molecule with speed vx traveling left and right to the end of the box by colliding with the end walls.

1. Time between collisions with the wall:

   $$t=\frac{2L}{v_x}$$

2. Frequency of collisions:

   $$f=\frac{1}{t}=\frac{1}{2L/v_x}=\frac{v_x}{2L}$$

3. Force according to Newton:

   $$F=\frac{dp}{dt}=ma$$

4. Change in momentum:

   $$\Delta{p}=mv_x-(-mv_x)=2mv_x$$

5. Average force in terms of particle velocity:

   $$\overline{F}=\Delta{p}(f)=2mv(\frac{v_x}{2L})=\frac{mv_x^2}{L}$$

6. Pressure for a single molecule:

   $$P_{1\:Molecule}=\frac{\overline{F}}{A}=(\frac{mv_x^2}{L})/A=\frac{mv_x^2}{LA}=\frac{mv_x^2}{V}$$

7. For N molecules traveling on x-axis:

   $$P_{N\:Molecules}=\frac{m}{V}(v_{x_1}^2+v_{x_2}^2+v_{x_3}^2....+v_{x_N}^2)=\sum_{a=0}^{N}\frac{mv_{x_a}^2}{V}$$

8. Using mean square speed:

   $$P_{N\:Particles}=\frac{Nm\overline{v_x^2}}{V}$$

9. Considering all three dimensions:

   $$\overline{v^2}=\overline{v^2_x}+\overline{v^2_y}+\overline{v^2_z}$$

   With equal distribution in all directions:

   $$\overline{v^2_x}=\overline{v^2_y}=\overline{v^2_z}$$

10. Final pressure equation in 3D:

    $$P=\frac{Nm\overline{v^2}}{3V}$$

11. Relating kinetic energy to temperature:

    $$E_{kinetic}=\frac{mv^2}{2}\propto{T}$$

12. Solving for kinetic energy:

    $$mv^2=2E_{kinetic}\Rightarrow\frac{mv^2}{3}=\frac{2E_{kinetic}}{3}$$

13. Introducing Boltzmann constant k:

    $$kT=\frac{mv^2}{3}=\frac{2E_{kinetic}}{3}$$

14. Combined pressure equation:

    $$P=\frac{N}{V}\frac{m\overline{v^2}}{3}=\frac{N}{V}\frac{2E_{kinetic}}{3}=\frac{N}{V}kT=\frac{NkT}{V}$$

15. Converting to moles using Avogadro's number:

    $$n=\frac{N}{N_a}$$
    $$R=N_ak$$

16. Final ideal gas law:

    $$P=\frac{nRT}{V}\Rightarrow{PV=nRT}$$